Принципи розв’язання статистичних задач
Відзначимо наступне: всі три критерії (Вальда, Севіджа і Гурвіца) були сформульовано для чистих стратегій, але кожний з них може бути поширений і на змішані, подібно тому, як це робиться в теорії ігор. Проте змішані стратегії в грі з природою мають лише обмежене (головним чином, теоретичне) значення. Якщо в грі проти свідомого супротивника змішані стратегії іноді мають сенс як «трюк», що вводить в оману супротивника, то в грі проти «байдужої природи» цей резон відпадає. Крім того, змішані стратегії придбавають значення тільки при багатократному повторенні гри. А якщо вже її повторюємо, то неминуче починають вимальовуватися якісь риси вірогідності ситуації, і ми ними можемо скористатися для того, щоб застосувати «стохастичний підхід» до задачі, а він змішаних стратегій не дає.
Крім того, в ситуаціях з «поганою невизначеністю», коли болісно не вистачає інформації, головна задача — цю інформацію отримати, а не вигадувати хитромудрі методи, що дозволяють без неї обійтися. Одна з основних задач теорії статистичних рішень — це якраз планування експерименту, мета якого — з'ясування або уточнення якихось даних.
Практична частина
Приклад 1
Уряд планує будівництво чотирьох типів електростанцій: ![]() (теплових),
(теплових), ![]() (пригребельних),
(пригребельних), ![]() (безшлюзових) і
(безшлюзових) і ![]() (шлюзових). Ефективність кожного з типів залежить від різних чинників: режиму річок, вартості палива і його перевезення і т.п. Необхідно вибрати самий оптимальний варіант.
(шлюзових). Ефективність кожного з типів залежить від різних чинників: режиму річок, вартості палива і його перевезення і т.п. Необхідно вибрати самий оптимальний варіант.
Розв‘язання
Припустимо, що виділено чотири різні стани, кожний з яких означає певне поєднання чинників, що впливають на ефективність енергетичних об'єктів. Стани природи позначимо через ![]() і
і ![]() . Економічна ефективність будівництва окремих типів електростанцій змінюється залежно від станів природи і задана матрицею:
. Економічна ефективність будівництва окремих типів електростанцій змінюється залежно від станів природи і задана матрицею:

Згідно критерію Вальда:
![]()
![]()
![]()
![]()
Тоді оскільки ![]() , то слід передбачити будівництво безшлюзової ГЕС (А3) .
, то слід передбачити будівництво безшлюзової ГЕС (А3) .
Скористаємося критерієм Севіджа. Побудуємо матрицю ризиків:

Покажемо як були отримані елементи матриці ризиків.
Оскільки ![]() , то:
, то:
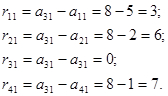
Поскольку ![]() , то:
, то:

Поскольку ![]() , то:
, то:

Поскольку ![]() , то:
, то:

Згідно критерію Севіджа визначаємо ![]() . Відповідно до цього критерію також передбачається будівництво безшлюзової ГЕС (А3) .
. Відповідно до цього критерію також передбачається будівництво безшлюзової ГЕС (А3) .
Скористаємося критерієм Гурвіца. Припустимо ![]() ;
;
тоді:
![]()
![]()
![]()
![]()
![]()
Отримаємо ![]() , тобто слід прийняти рішення про будівництво пригребельних ГЭС(
, тобто слід прийняти рішення про будівництво пригребельних ГЭС(![]() ). Якщо ж припустити відомим розподіли вірогідності для різних станів природи, наприклад, якщо вважати ці стани рівноімовірними (
). Якщо ж припустити відомим розподіли вірогідності для різних станів природи, наприклад, якщо вважати ці стани рівноімовірними (![]() ), то для ухвалення рішення слід знайти математичне очікування виграшу:
), то для ухвалення рішення слід знайти математичне очікування виграшу:
![]()
![]()
![]()
![]()
Оскільки максимальне значення має М 3, то слід вибрати рішення А3.
Інші статті по менеджменту
Розробка організаційної структури управління на транспортному підприємстві
На кожному етапі
розвитку економіки переважне поширення одержують ті або інші типи виробничих
організацій. Як у народному господарстві так і на транспорті відбувається
безупинне удоскон ...
Удосконалення процесу очищення соняшникової олії (електромагнімним способом)
Гроші… Сьогодні мабуть нема такої теми, розмови яка б прямо чи частково
не стосувалось цього слова. Стан матеріального забезпечення головна проблема
будь-якого підприємства, господарства ...
Аналіз зовнішнього середовища підприємства
Актуальність теми обумовлена тим, що сучасне зовнішнє середовище підприємств характеризується надзвичайно високим рівнем складності, динамізму і невизначеності. Здатність пристосовуватися до змін в зо ...